How to build a cyclic polyrhythm from one parameter

What types of parameters can we use to construct a cyclic polyrhythm?

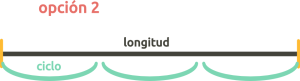
We can construct a cyclic polyrhythm from one of the following parameters:

 

the cycle must be equal to the given length	the cycle must be contained and synchronized to the given length	given ratio

 

• the length of the cycle
• the length of a succesion, segment or idea
• the ratio of the polyrhythmic cycle

 

---

1. Build from a cycle length
2. Construct from the length of a succesion, segment or idea.
3. Building from a ratio

---

 

BUILD FROM A CYCLE LENGTH

Earlier we have seen how to calculate the length of the polyrhythmic cycle from given rhythmic voices, defined with fixed fractions and iT. The reverse process is also possible: starting from a cycle length, we can calculate all possible cyclic polyrhythmias that coincide with this length.

In the case of a two-voice polyrhythm, the numerator of the fraction resulting from voice 1 must be equal to the length of the cycle. For this to happen, we have two options (in both, any denominator is possible):

1. Start from a fraction with numerator equal to the length and use an iT (1). (Remember that in the Nuzic app it is only possible to use single-digit numerators).
2. Choose a numerator and a fixed iT whose multiplied values equal the length.

Use the factor calculator in the references on the side, to find all possible options. Let’s look at the following examples:

 

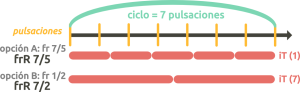(In the Nuzic app we cannot perform option A, as numerators of more than one digit are not allowed).

 

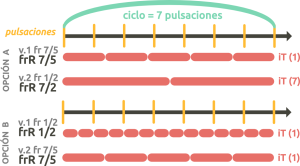
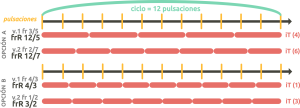
In the case of a three-voice polyrhythm, the least common multiple of the numerators of the frR of voice 1 and voice 2 must be equal to the length. Here we also have two options. In both, any denominator is possible:

1. Start from two FrR whose numerators are equal to the length.
2. Start from two FrR with different numerators whose least common multiple equals the length.

Let’s look at the following examples:

 

 

TO BUILD FROM A SEGMENT LENGTH, SUCCESION OR IDEA

Here we also start from a given length (of a succesion, segment or idea), and we want to calculate all the possible cyclic polyrhythms that we could fit into it. It is a process similar to the previous section, but with more possibilities since we can repeat one or more times the polyrhythmic cycle, with the only condition that the end of the last cycle is synchronized with the end of the succession, segment or idea. This prevents the cycle from being interrupted (it would give an error in the app).

To perform this calculation, we follow the steps below, whether it is a two-voice or three-voice polyrhythm:

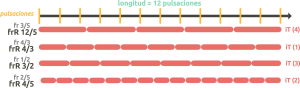
1. We decompose into prime factors the number of the given length (use the calculator on the side referents) → . Ex: length 12 = 2x2x3.
2. We calculate all the options resulting from multiplying the factors with each other and include the number 1 → 1. Ex above: 1, 2, 3, 4, 6 and 12.
3. We define the numerators of the frR of the voice(s) using any of the figures obtained in step two (any denominator is possible) → frR 12/5, 4/3, 3/2, 4/5, etc….. Ex above: possible frR of the voices in a length of 12 pls → frR 12/5, 4/3, 3/2, 4/5, etc….

 

 

BUILD FROM A RATIO

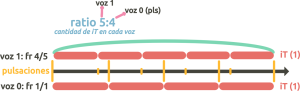
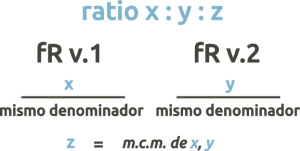
We have also seen how to obtain the ratio of a polyrhythmic cycle from the fractions and fixed iT of the rhythmic voices. Here the reverse process would be to start from a ratio and see what polyrhythms we could construct with that ratio.

In 2-voice polyrhythms we have only one option: in the fraction resulting from voice 1 you will use the 2nd number of the ratio as numerator, and the 1st as denominator. / Eg: ratio 5:4 → frR voice 1 = 4/5

 

 

In the 3-voice polyrhythms we have different options with their variants:

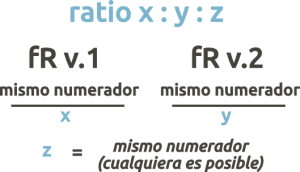
1. Ratio in denominators, same numerator
   • Variant: multiplication of the ratio numbers by the same number
2. Ratio in numerators, same denominator
   • Variant: multiplication of the ratio numbers by the same number
3. Factorization of the ratio numbers, and distribution between numerators and denominators

Each option will be discussed in more detail below:

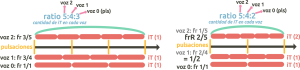
• The ratio numbers are placed in the denominators of voices 1 and 2. Both fractions have the same numerator (can be any number), and frR is reduced if possible.

 

 

Let’s look at the following example with the 5:4 ratio:

 

 

• • A variant of the previous case: the ratio numbers of the denominators can be multiplied by the same number. When the ratio relates only voices 1 and 2, it creates a secondary cycle. Let’s see the following example with the ratio 3:2, where we multiply x2 the denominators of the initial fractions 5/3 and 5/2:
    

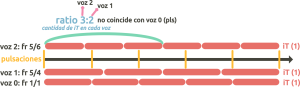
frR 5/6 and 5/4 → denominators x2 ; (could also be frR 5/9 and 5/6 → denominators x3, etc.)

 

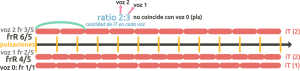
• Ratio numbers are placed in the numerators of voices 1 and 2. Both fractions have the same denominator (can be any number), and frR is reduced if possible. When the ratio relates only voices 1 and 2, it creates a secondary cycle.

 

Let’s look at the following example with the 2:3 ratio:

 

 

• • A variant of the previous case: the ratio numbers of the numerators can be multiplied by the same number. Remember that when the ratio relates only voices 1 and 2, it creates a secondary cycle. Let’s see the following example with the ratio 2:3, where we multiply x2 the numerators of the initial fractions 2/5 and 3/5:

frR 5/6 and 5/4 → numerators x2 ; (could also be frR 6/5 and 9/5 → denominators x3, etc.)

 

• When the ratio numbers can be decomposed into prime factors, we can distribute them between the numerators and denominators of the fractions of voices 1 and 2:

 

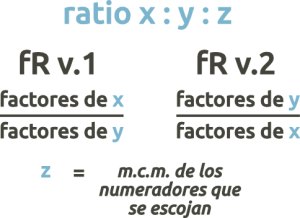
The length of the cycle will depend on how you distribute the numbers in the numerators. You can use the prime factorization calculator in the side reference to decompose the ratio numbers into prime factors. Let’s look at the following example with the ratio 21:20:

 

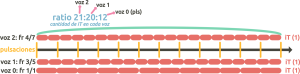
Decomposition into prime factors: 21=3×7 and 20=5x2x2x2 → frR v.1 = 3/5, and frR v.2 = 4/7 (cycle length = m.c.m. of numerators = 12 beats)