Musical operations are a compositional resource that allows us to generate and develop new variations based on a initial succession of elements. Using numbers to represent the elements of a sequence allows us to perform simple arithmetic operations with great ease.

If we listen to the same succession repeated exactly the same several times, it generates a sensation of monotony, and we are no longer interested in it. If we want to avoid the feeling of monotony, we will seek to vary it in some way, and to a greater or lesser degree.

The sense of musical operations is to avoid exact repetition, through the development of new variations. Through the operations, we can control the degree of contrast or continuity that we want to give to our musical ideas, bringing variability and diversity to our compositional material, without losing the identity of the initial musical idea.

TYPES OF OPERATIONS

We define three types of musical operations:

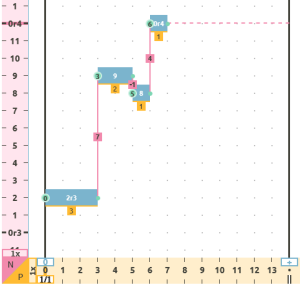
• Displacement (DES): The elements of the initial succession change their numerical value to create the new variation, thus producing a displacement of the elements, but conserving the same number (of elements).

opening melody audio

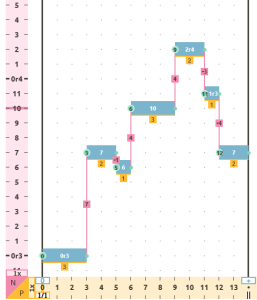
initial melody with +2 shift in all Notes audio

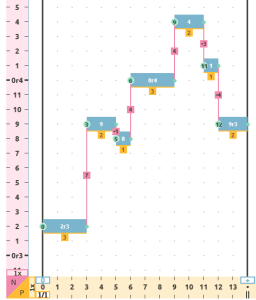
• Fusion (FUS): The elements of two original sequences are merged to create a new variation containing the elements of both sequences. This operation can be applied vertically, i.e., between 2 simultaneous sequences, either monophonic or polyphonic, or horizontally when applied to two consecutive sequences in time.

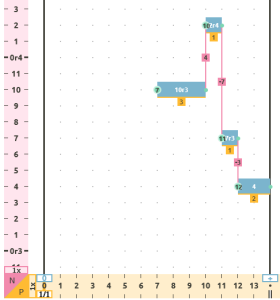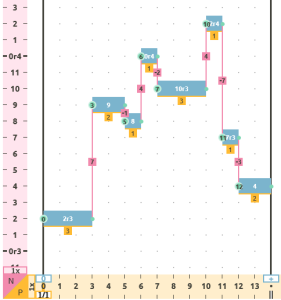audio

audio

audio

• Permutation (PER): The new variation has the same elements as the original sequence but with the order changed.
  

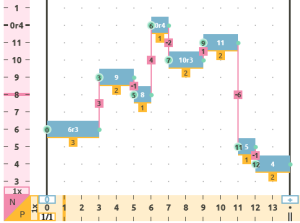
original melody audio

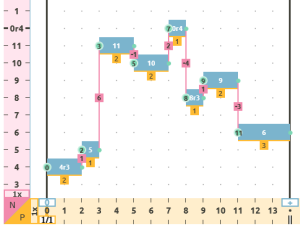
melody permuted in Notes and iT audio

It is important to know that each of the operations produces a specific sound effect on the original sequence.

For example, if we decide to apply a displacement operation to a sequence of Notes, we know that if we apply a sum of +4 to all the Notes, we will obtain a variation that is a transposition 4 semitones sharper. On the other hand, if we apply a subtraction of -4, we will obtain a variation that is a transposition 4 semitones lower.

The operations are an example of the flexibility of numbers, since they can be applied on successions of elements of any type (Notes, iS, Pulses, iTs…).